深度學習中的優化技巧 - 批次標準化 (Batch Normalization, BN)
核心目標:改變誤差曲面 (Error Surface) 的地貌�
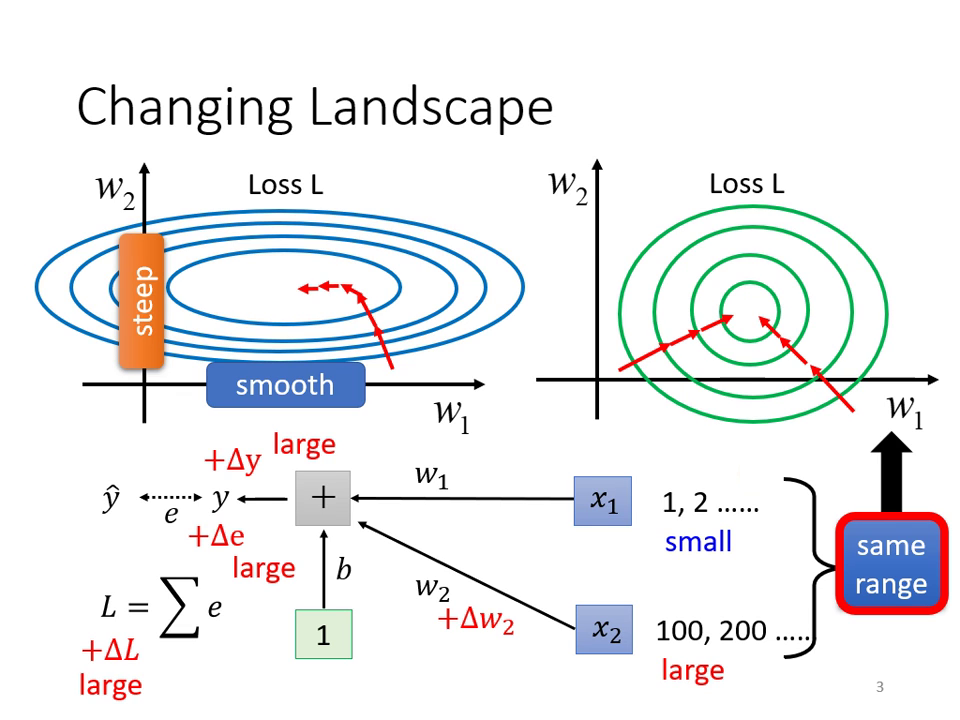
在優化過程中,如果誤差曲面非常崎嶇(例如在某些參數方向斜率變化極小,在另一些方向斜率極大),即使是簡單的模型也很難訓練。 Batch Normalization 的本質就是「把山剷平」,讓誤差曲面變得比較平滑且不崎嶇,進而使訓練變得更容易。
為什麼誤差曲面會崎嶇?
- 輸入特徵的尺度 (Scale) 差異: 當輸入特徵 的數值範圍差距很大時,對應的參數 對 Loss 的影響力(斜率)也會產生巨大差異。
- 深層網路的連鎖反應: 即使輸入層做了標準化,經過第一層權重 運算後,輸出的分佈可能又會變得混亂,導致後續層級(如 )的訓練依舊困難。
運作機制:特徵標準化 (Feature Normalization)
為了讓不同維度的特徵具有相似的數值範圍,我們會進行以下處理:
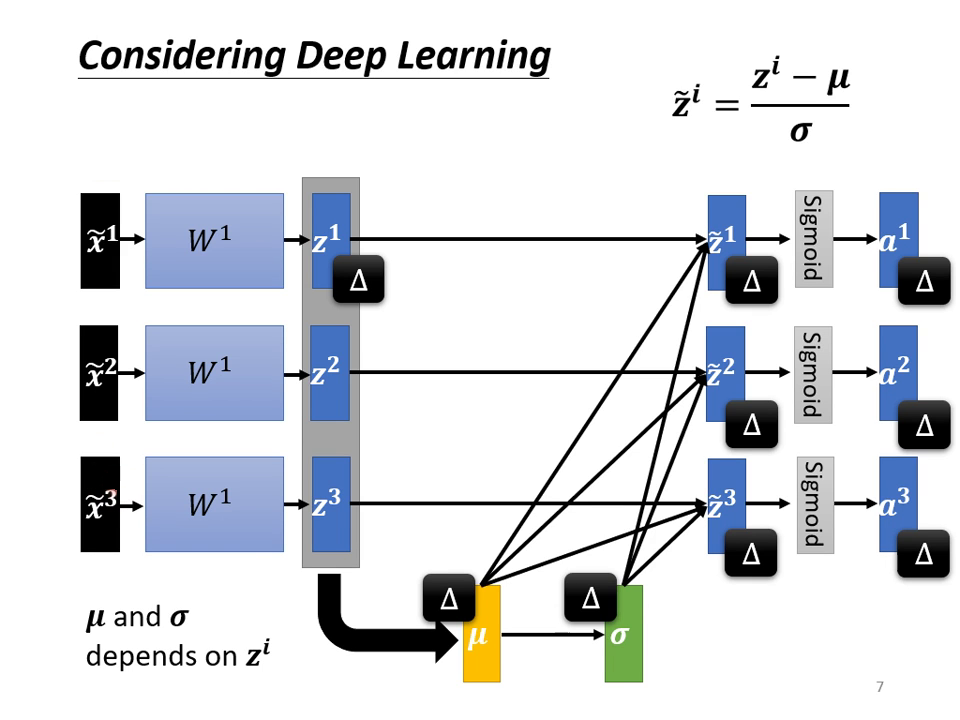
- 計算平均值 () 與標準差 (): 針對每一個維度,計算該批次資料的平均值與標準差。
- 標準化 (Standardization): 將數值減去平均值並除以標準差,得到平均值為 0、變異數 (Variance) 為 1 的新分佈。
- 擺放位置: 在實作上,標準化可以放在激活函數(Activation Function)之前 () 或之後 (),兩者差異不大。若使用 Sigmoid,建議放在 處以維持在斜率較大的區域。
 |  |
|---|---|
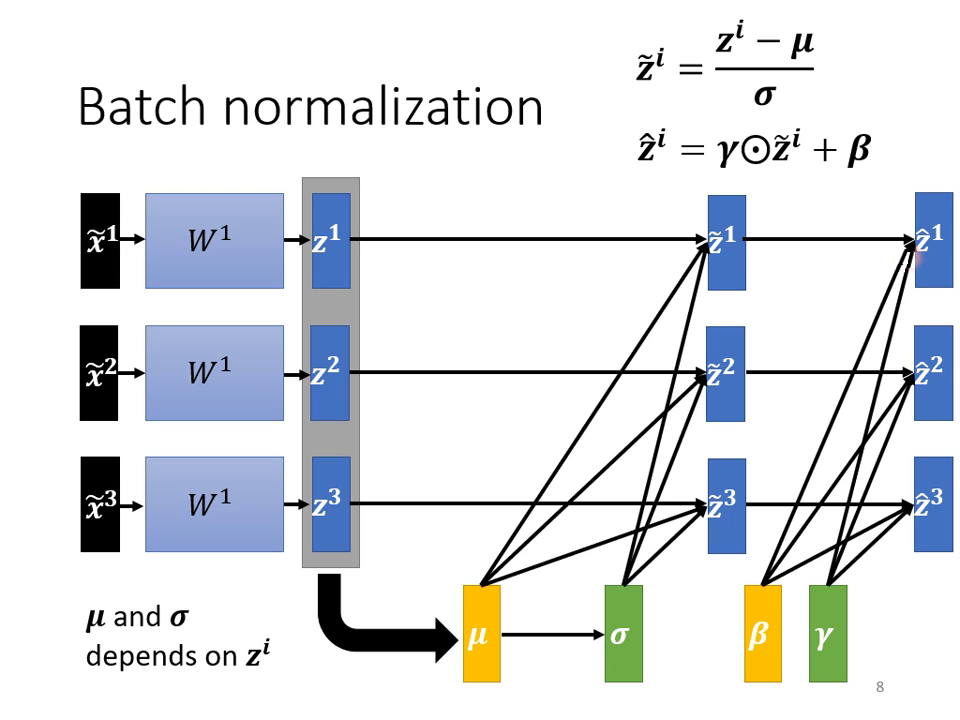
| 對向量的對應 element 做求平均�、標準差的運算,求得向量 | 對每個向量 利用 對對應 element 進行歸一化,得到 |
為什麼稱為「批次 (Batch)」標準化?
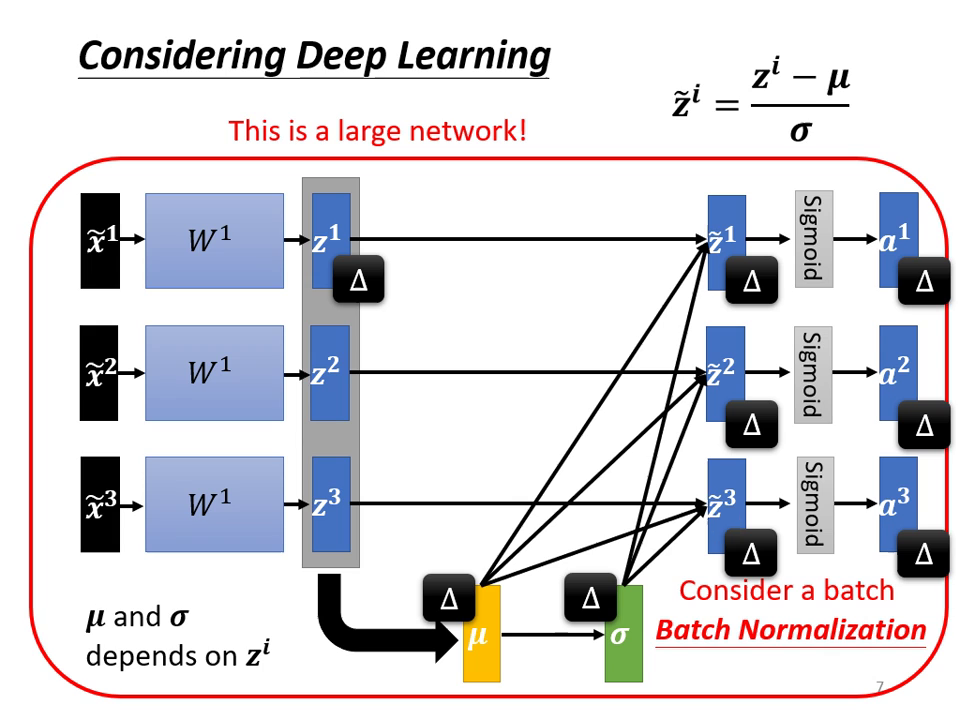
- 實務限制: 理想上應對整個資料集進行標準化,但因 GPU 記憶體無法一次讀取百萬筆資料,實務上改為對一個 Mini-batch 內的資料計算 與 作為近似。
- 參數關聯性: 做了 BN 後,同一個 Batch 內的不同資料會變得彼此關聯(因為它們共用同一組 與 )。
- 學習參數 ( 與 ): 標準化後會再乘上 並加上 ,這兩個是由網路學習出來的參數,讓模型有能力調整輸出的分佈,而不被強制鎖定在平均值 0。
 |  |
|---|---|
| Mini-batch 估計 造成樣本間關聯 | 可學習參數 讓標準化輸出保有彈性 |
測試階段 (Testing/Inference) 的處理
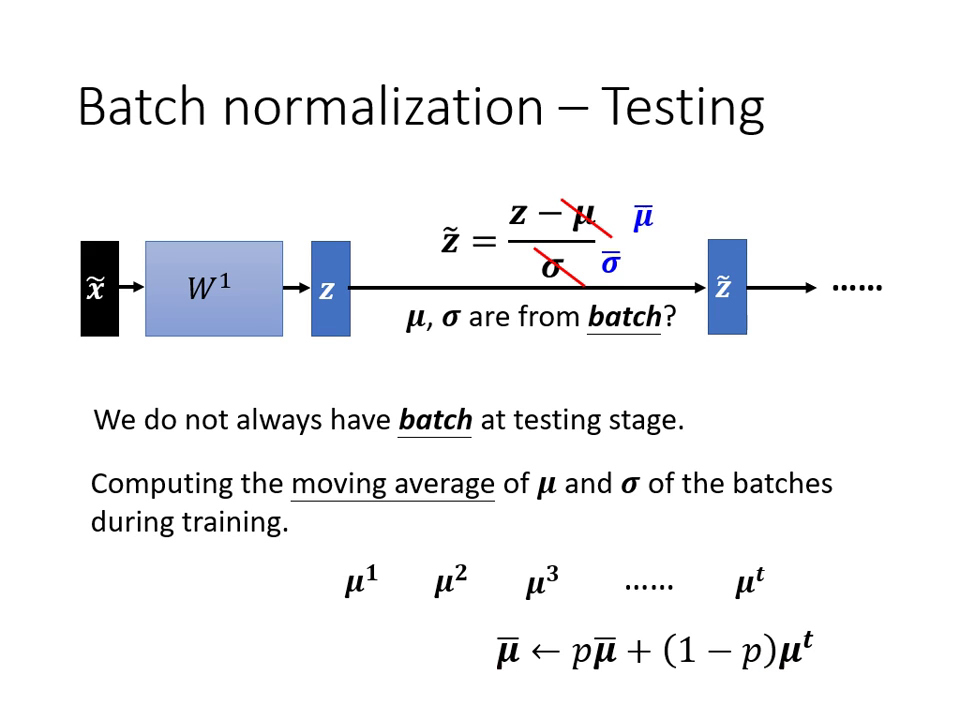
在測試時通常只有單筆資料,無法計算 Batch 的 與 。
- 解決方案: 在訓練過程中計算 與 的 移動平均 (Moving Average)。
- 執行方式: 測試時直接套用訓練階段累積下來的平均值 () 與標準差 () 進行運算。
Batch Normalization 的優點與爭議
- 具體優點:
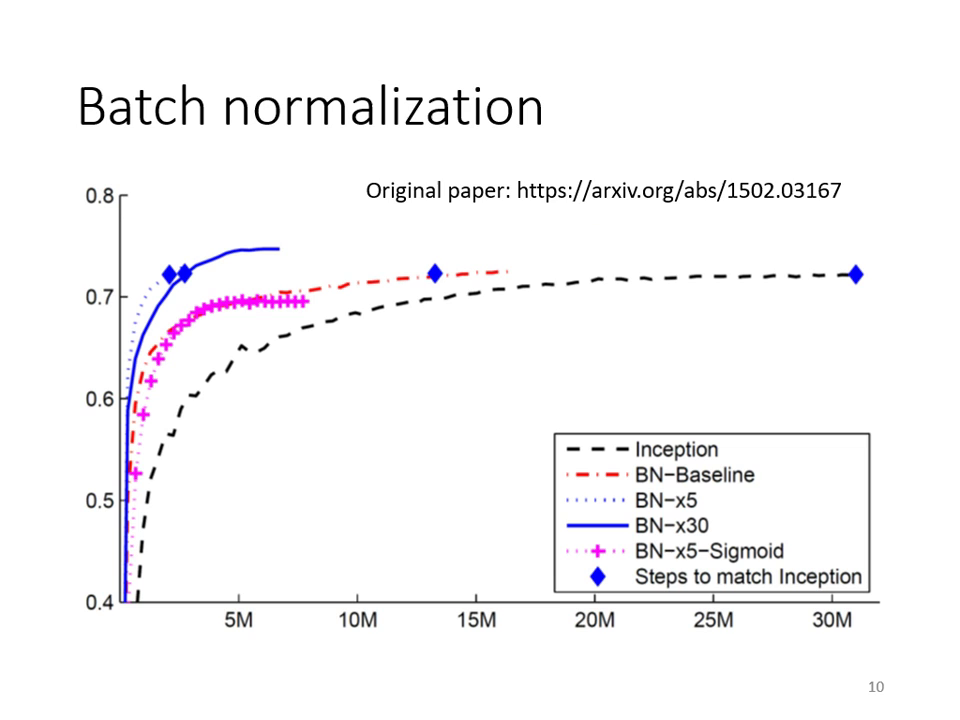
- 加速訓練: 達到相同正確率所需的時間大幅縮短。
- 容許更高的學習率 (Learning Rate): 因為曲面變平滑了。
- 改善收斂: 讓原本難以訓練的 Sigmoid 網路也能成功訓練。
- 理論爭議:
- 原始論文認為 BN 有用是因為解決了 Internal Covariate Shift(內部協變量偏移)。
- 後續研究打臉了上述觀點,認為 BN 最關鍵的作用是改變了 Error Surface 的平滑度。