深度學習中的優化技巧 - 分類 (Classification)
當我們將問題從回歸 (Regression) 轉向分類時,目標不再是輸出一個單一數值,而是要判斷輸入屬於哪一個類別。
類別的表示方式:從數值到 One-hot Vector
在做分類時,我們必須將「類別」數位化。
- 直接編號法 (瑕疵方法): 將 Class 1 設為 1,Class 2 設為 2,以此類推。這會隱含一個假設:認為 Class 1 與 Class 2 較近,而與 Class 3 較遠。如果類別間沒有這種序位關係(例如:預測貓、狗、鳥),這種表示法會誤導模型。
- 獨熱向量 (One-hot Vector):
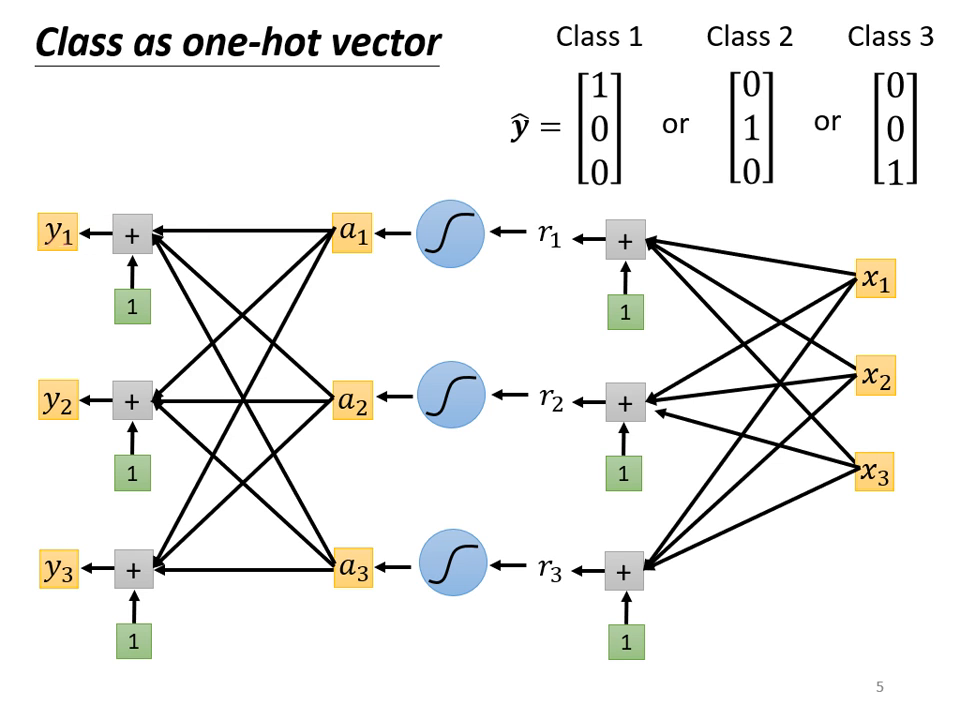
這是最常見的做法。如果有三個類別,正確答案(Label )就是一個三維向量。
- 優點: 任何兩個類別之間的距離都是一樣的,不會預設類別間的親疏關係。
 |  |
|---|---|
| 直接編號法 (瑕疵方法) | 獨熱向量 (One-hot Vector) |
網路結構的調整
為了對應 One-hot vector,神經網路的輸出層也必須輸出同樣維度的向量(例如輸出三個數值 )。
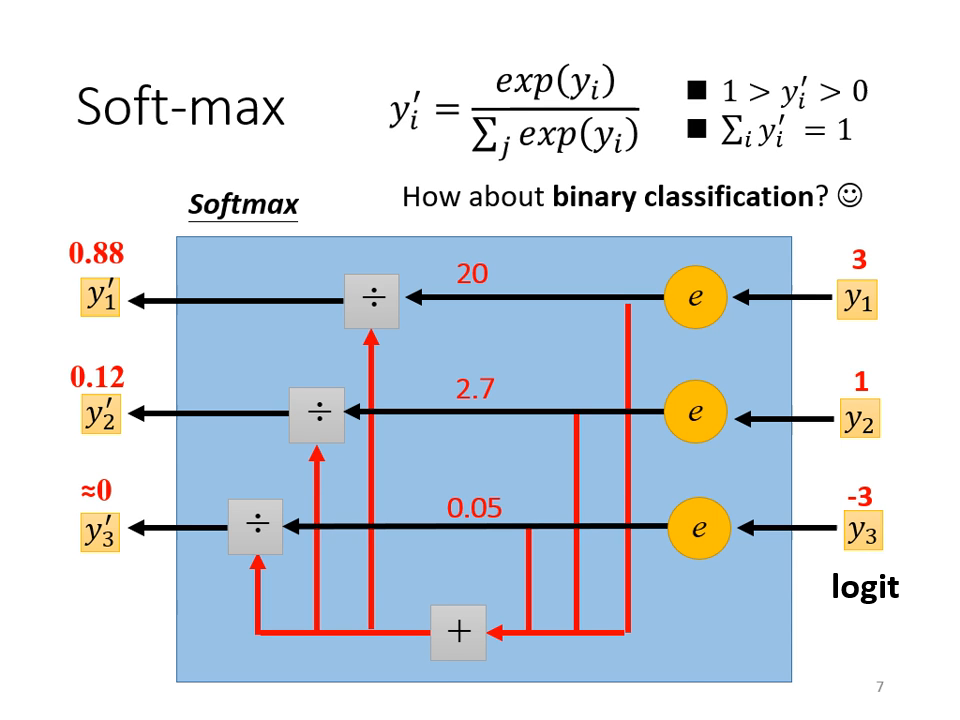
Soft-max 層的作用
在分類問題中,通常會在網路的最後輸出加上 Soft-max 函數。
- 主要功能:
- 歸一化 (Normalization): 將輸出值轉化為 0 到 1 之間,且所有輸出的總和等於 1。這讓輸出可以被視為一種機率分佈。
- 拉大差距: 透過取指數 (),Soft-max 會強化較大的值並抑制較小的值。
- 與 Sigmoid 的關係: 當類別只有兩個時,使用 Soft-max 與使用 Sigmoid 是數學上等價的。
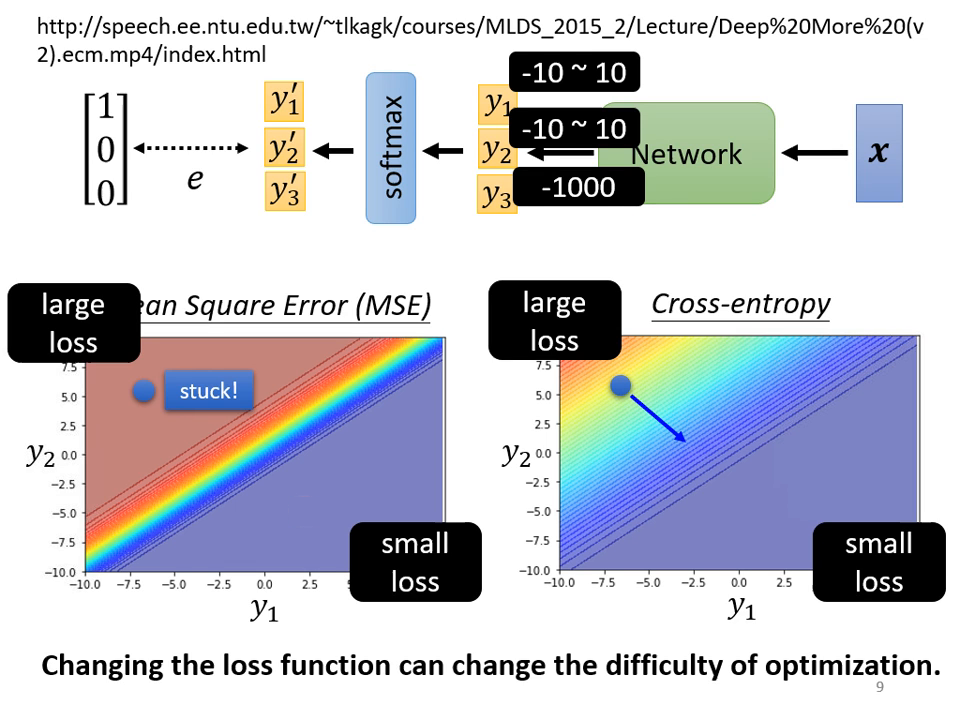
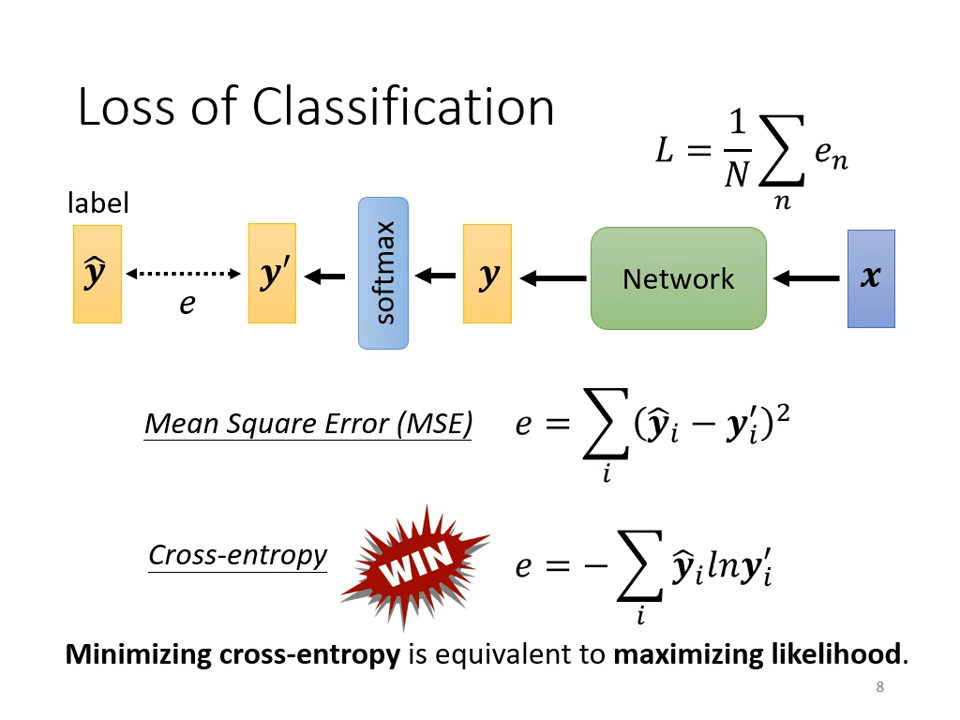
損失函數 (Loss Function):MSE vs. Cross-entropy
計算預測值 與�正確答案 之間的距離時,有兩種主要選擇:
- 均方誤差 (Mean Square Error, MSE): 計算各個元素的平方和。
- 交叉熵 (Cross-entropy): 公式為 。在數學上,最小化 Cross-entropy 等同於最大化似然估計 (Maximize Likelihood)。
為什麼分類首選 Cross-entropy?(優化角度)
從 Error Surface (誤差曲面) 的形狀來看,Cross-entropy 顯著優於 MSE:
- MSE 的困境: 當模型預測極度錯誤(Loss 很大)時,MSE 的地形非常平坦,梯度 (Gradient) 趨近於零。這會導致訓練初期就卡住,難以起步。
- Cross-entropy 的優勢: 即使在 Loss 很大的地方,它依然保有斜率。這讓模型能順著梯度快速往正確方向移動。
- 實務注意: 在 PyTorch 等框架中,
CrossEntropyLoss通常已內建 Soft-max 運算,使用者不需要在網路層中重複添加。